1/2

2026/01/02

Three.js

シェーダーに定数を渡すjs

//シェーダー内で#define BOUNDS 800.00として使用可能になる
...material.defines.BOUNDS = 800.0;

~~

~~ はビット演算子の二重否定で、Math.floor() の高速版。

// 正の数の場合、Math.floor()と同じ動作
~~(5.7)  // => 5
~~(5.2)  // => 5
~~(10.9) // => 10

// Math.floor()との比較
Math.floor(5.7)  // => 5
Math.floor(5.2)  // => 5

変換行列

3Dでオブジェクトを移動させるときは「変換」呼ばれる数学演算を使う。
3つの基本的な変換 position,rotate,scale
Object3Dを継承しているやつは全部これら使える。ジオメトリやマテリアルにはない。

rotate

回転の順序が重要になる。同じ値で回転させても順番で違う結果になる。
そのため、positionやscaleで使えるVector3()では不十分。

3つの引数に加えて第４引数に順序を追加したEuler()がある。

変換行列

オブジェクトの移動、回転、拡大は一つの行列に統合される。行列はCPUとGPUにとって、個々の変換よりもはるかに効率的。
何も指定ない状態の変換行列は4*4の単位行列になっている。

対角成分が 1 で、それ以外の成分が 0 である正方行列を単位行列という。
単位行列をベクトル x に掛けても、ベクトルは変化しない。

実際には、すべてのオブジェクトには2つの変換行列が存在。

ローカル行列であり、オブジェクトの.position、.rotation、.scaleを統合した値を保持。
ローカル行列はObject3D.matrixプロパティに格納されている。Object3Dを継承するすべてのオブジェクトがこのプロパティを持つ。
ワールド行列。Object3D.matrixWorldに保存されている。

meshAにposition.xが3あり、その子meshBにposition.xが3という変換されていると、meshBはsceneからみてx = 6の位置にある。その情報はワールド行列にある。

4*4変換行列にたいしてのscaleとpositionの変換はこうなる。

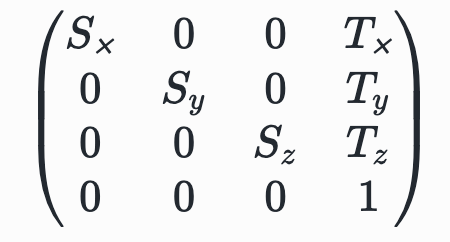
rotateはちょいムズで、3Dの回転は 3×3行列で表される。

行列の読み方

行列の掛け算↓

[ 1   0       0      ]   [ x ]   [ 1×x + 0×y + 0×z ]
[ 0   cosθ    -sinθ  ] × [ y ] = [ 0×x + cosθ×y + (-sinθ)×z ]
[ 0   sinθ     cosθ  ]   [ z ]   [ 0×x + sinθ×y + cosθ×z ]

式として↓

x' = x
y' = y cosθ - z sinθ
z' = y sinθ + z cosθ

また、three.jsでは行列の列は新しい座標軸を表す。
つまり、上の計算は以下のようにも解釈できる。

x' = x × [1, 0, 0]^T のX成分 + y × [0, cosθ, sinθ]^T のX成分 + z × [0, -sinθ, cosθ]^T のX成分
      = x × 1 + y × 0 + z × 0
      = x

y' = x × [1, 0, 0]^T のY成分 + y × [0, cosθ, sinθ]^T のY成分 + z × [0, -sinθ, cosθ]^T のY成分
      = x × 0 + y × cosθ + z × (-sinθ)
      = y cosθ - z sinθ

z' = x × [1, 0, 0]^T のZ成分 + y × [0, cosθ, sinθ]^T のZ成分 + z × [0, -sinθ, cosθ]^T のZ成分
      = x × 0 + y × sinθ + z × cosθ
      = y sinθ + z cosθ

軸回転の解説

x軸回転：x軸を固定してYZ平面を回転。
→x座標は変わらない

R_x(θ) = [ 1   0        0     ]
         [ 0   cosθ    -sinθ  ]
         [ 0   sinθ     cosθ  ]

１列目（x座標）は変わっていない。

余弦定理

ヨビノリ様の動画参考に
https://www.youtube.com/watch?v=2kZNmm4AG7I

式を理解するための加法定理を理解するための余弦定理をまず復習。
余弦定理→三平方の定理の拡張で、直角三角形に依らなくしたもの。

斜辺aとしたら
a² = b² + c² - 2bc・cosθ

加法定理

参考
https://www.youtube.com/watch?v=B7OSM0M6wkA
https://medgadget-freak.com/math-addition-theorem/

x軸回転に戻る

まずYZ平面で考える。

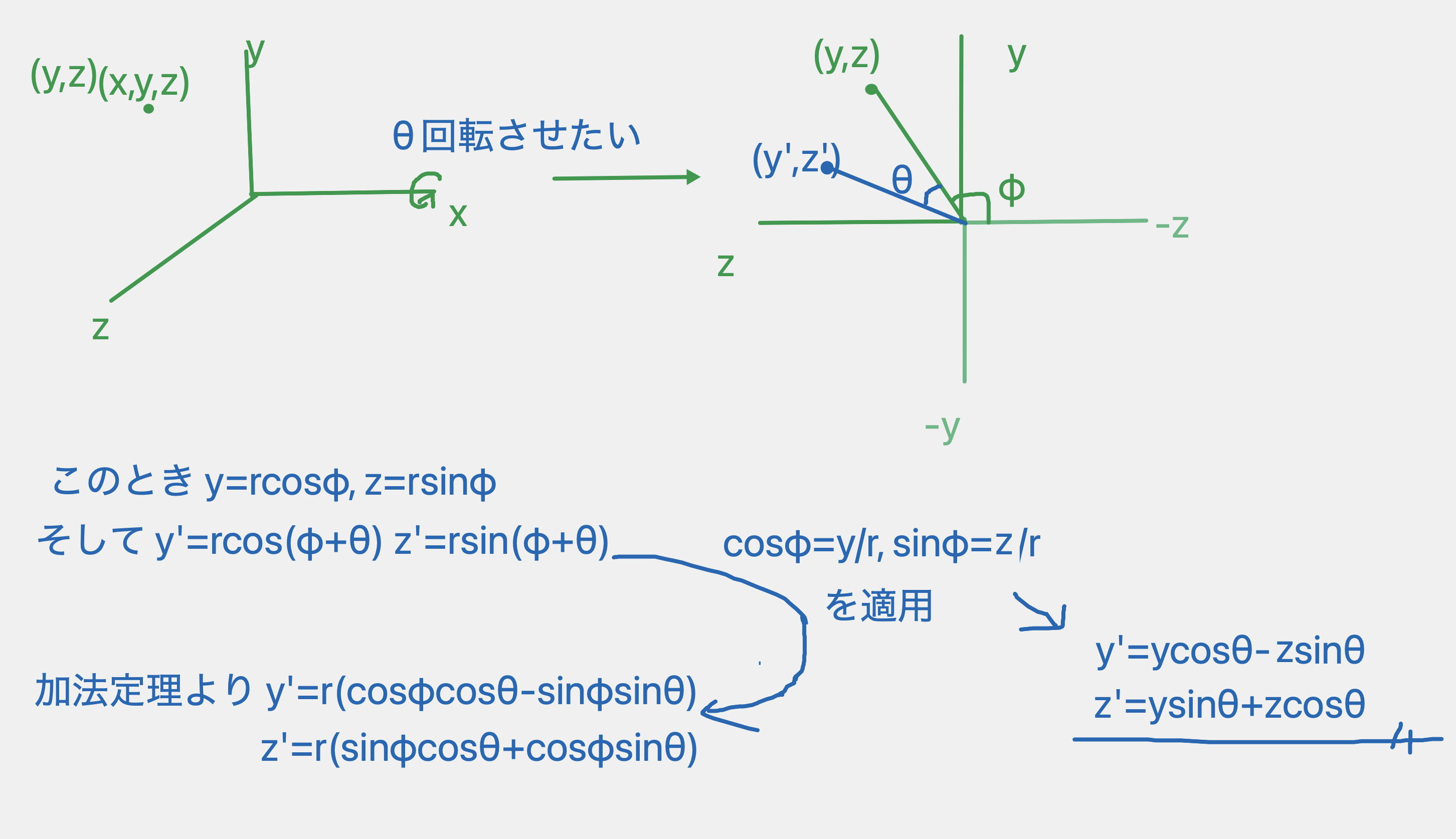
上の図のように、x軸をθ回転させた時
y → y cosθ - z sinθ
z → y sinθ + z cosθ

感想

いやむずすぎ。でもこれ毎日やる。

It is way too hard. but I'll try it everyday.

‹

1/1

日記

2026/01/01

›

1/3

日記

2026/01/03